An Illustrated Guide to All 3 Main Types of Symmetry (and 24 Variations)

0 symmetry

As someone who’s not a mathematician, I’ve often found it challenging to find clear, visual explanations of the different types of symmetry that exist. When I first started exploring the concept of symmetry, I was surprised by how many symmetry patterns there actually are—and how tricky it can be to understand each one. From the symmetry in geometry that we learn about in school to the beautiful symmetry in nature and art, the idea of symmetry shows up everywhere, but the explanations aren’t always easy to follow.

In this guide, I’ve set out to simplify these concepts by illustrating each of the main types of symmetry in a way that anyone can understand, without needing a math degree. We’ll look at familiar examples like line symmetry and rotational symmetry, and dive into some of the more complex types that you might not know about.

Whether you’re curious about the symmetry found in nature, designing something symmetrical yourself, or just trying to wrap your head around the concept, I hope this illustrated guide can be of help.

Previous Art

First of all, here are a few good resources I found:

Plane Symmetry - University of York
The 17 Wallpaper Groups - Xah Lee Web
About Symmetries of the Plane - Hobart and William Smith Colleges
2D Symmetry Groups - University of Washington (good visuals to understand how each symmetry is constructed)
Basic Tilings: The 17 Wallpaper Groups - John J. G. Savard

I had to use all of the above to fully understand all the different types of symmetry.

(Note: Please keep in time that I am not a mathematician so all you are reading are over-simplifications that might or might not be completely (in?)accurate.)

At some point, I came across the claim that there are 17 types of symmetry. This set me off to find them all and get a good visual for each. Well, it was easier said than done. Even the claim that there were 17, was difficult to pin down in detail.

Basic transformations

First things first. Here are the basic transform operations on which all symmetries are based:

1. Translation
1. Rotation
1. Reflection

The last one from the books is:

1. Glide Reflection

This is the combination of a translation and reflection (but it is neither one alone.)

According to Wikipedia, there are two categories of motions:

Direct, proper or rigid: translations and rotations that preserve the orientation shape.
Indirect or improper: reflections and glide reflections that invert the orientation of a shape.

I have also found literature calling them all “Rigid Motions of the Plane”. According to one source “it is a matter of convention whether the orientation-reversing maps such as reflections are considered ‘proper’ rigid motions.”

High-level categories

One site that helped me understand the higher level of categorization was this page from the Math department at the University of York: https://www.york.ac.uk/depts/maths/histstat/symmetry/welcome.htm

There appear to be 3 main groups of symmetry on a plane:

Rotational Symmetries: around a point, including identity and mirror symmetries.
Frieze Symmetries: sequences along a line
Wallpaper Symmetries: tiling across the plane

Per Wikipedia “there are three kinds of symmetry groups of the plane”:

2 families of rosette groups – 2D point groups

7 frieze groups – 2D line groups

17 wallpaper groups – 2D space groups.

Thinking of those as 0-D, 1-D and 2-D (0-dimensions, 1-dimension and 2-dimensions) helped memorization.

Now onto that magic number: 17. There are 17 ways to tile the plane using a pattern. These are symmetric tessellations also called wallpaper. Wikipedia has an explanation on why there are exactly seventeen groups (for smart people, needless to say).

Visualizing Symmetries

To show how all symmetries work I’ll use a paperclip. It is a simple item, and readily available if one wants to try this at home. I have marked one end of the paperclip with three red lines for easier differentiation.

The groups are labeled using the Crystallographic notation.

It all starts with the identity symmetry (I’m convinced Mathematicians love to include identity operations in lists). Is is technically correct to include identity symmetry in our list? Yes. Is is pedantic? Also yes.

Point Groups: Rigid or Rotational Symmetries (0-D)

Conventionally called “rotational” symmetries. I like using the term “rigid” instead to be more clear and inclusive.

There is an infinite number of rotational symmetries, since there is an infinite number of angles we could rotate an object around a point.

m
2
g (glide)
2mm
3
3m
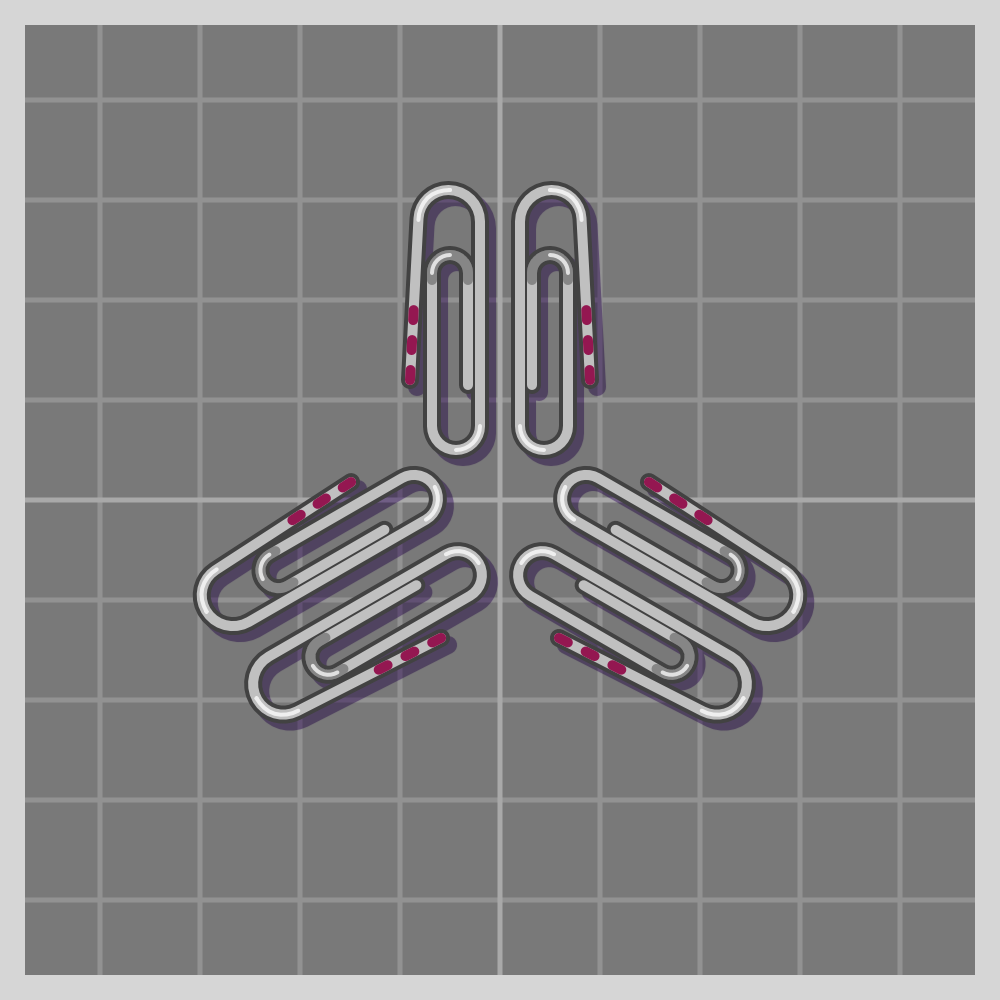
4
4m (4mm)

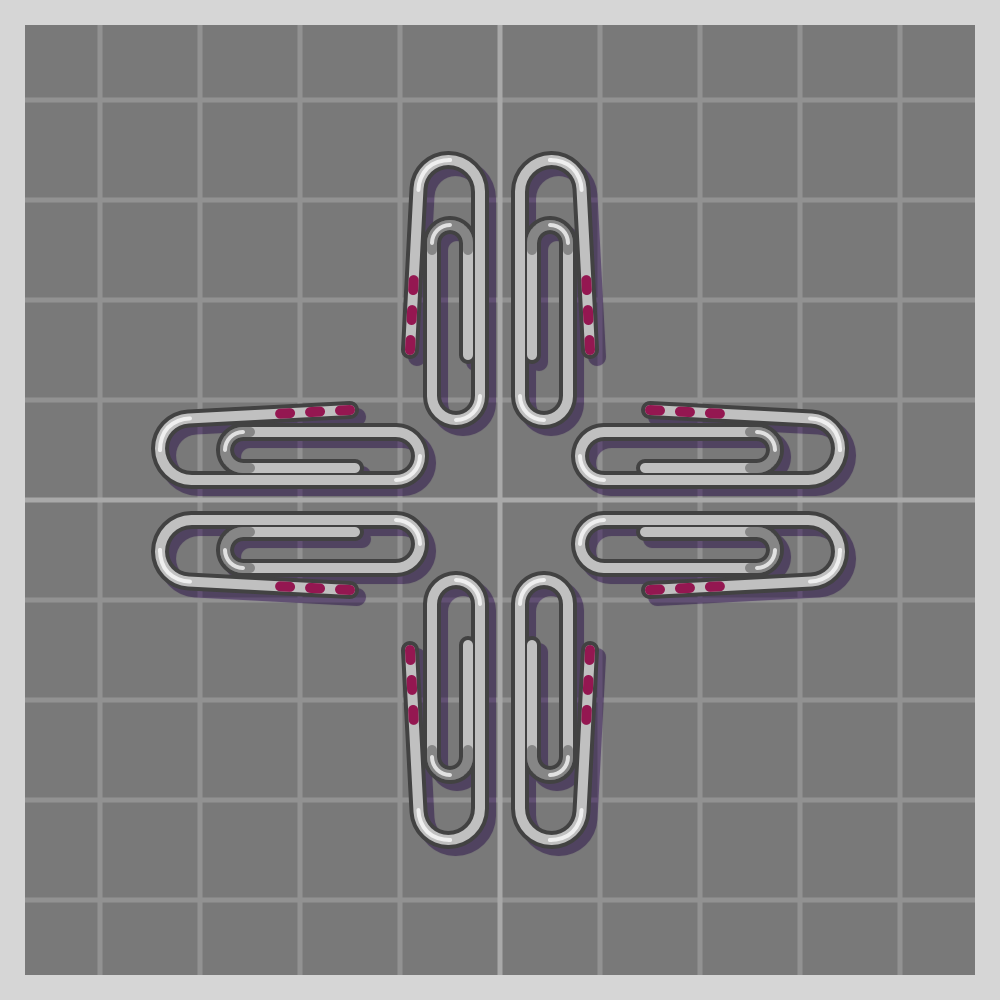
Line Groups: Symmetries: Frieze (1-D)

Per Wikipedia’s definition the Frieze group is “a two-dimensional design that repeats in one direction.”

There are seven types of Frieze symmetries.

t
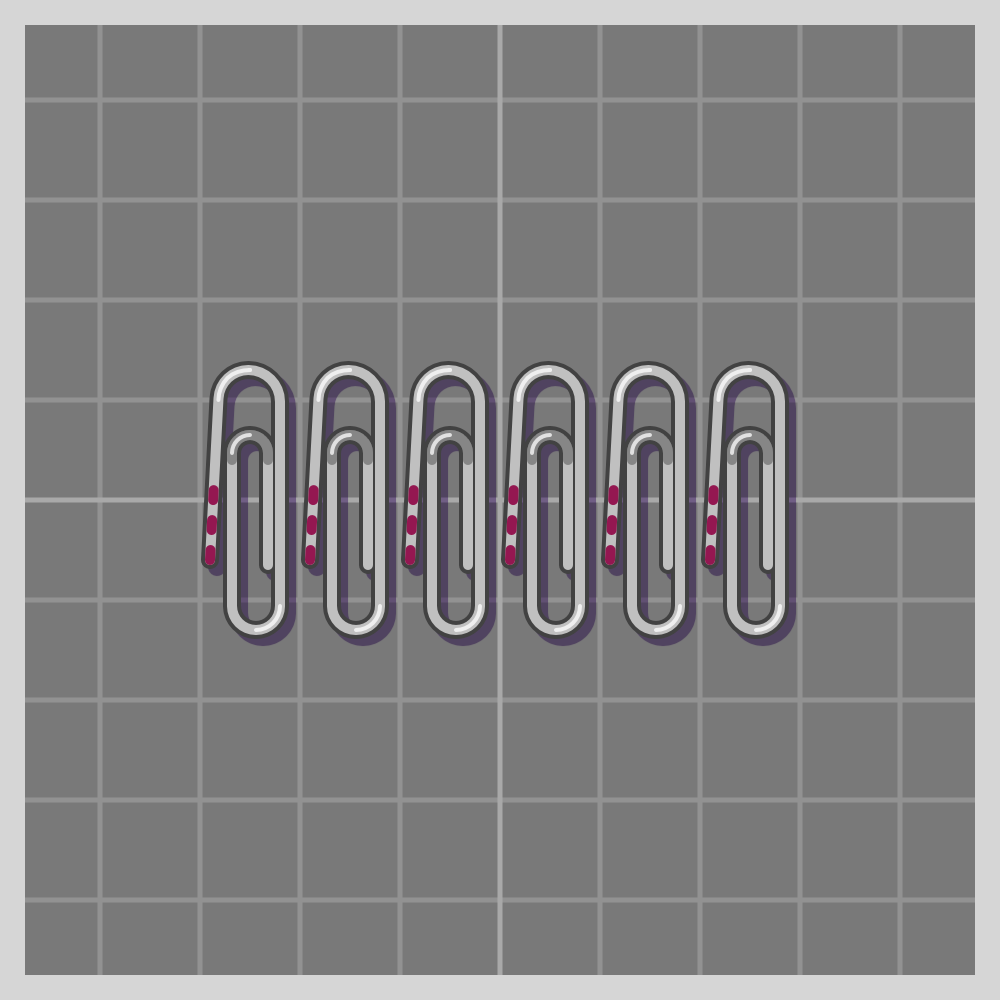
tm
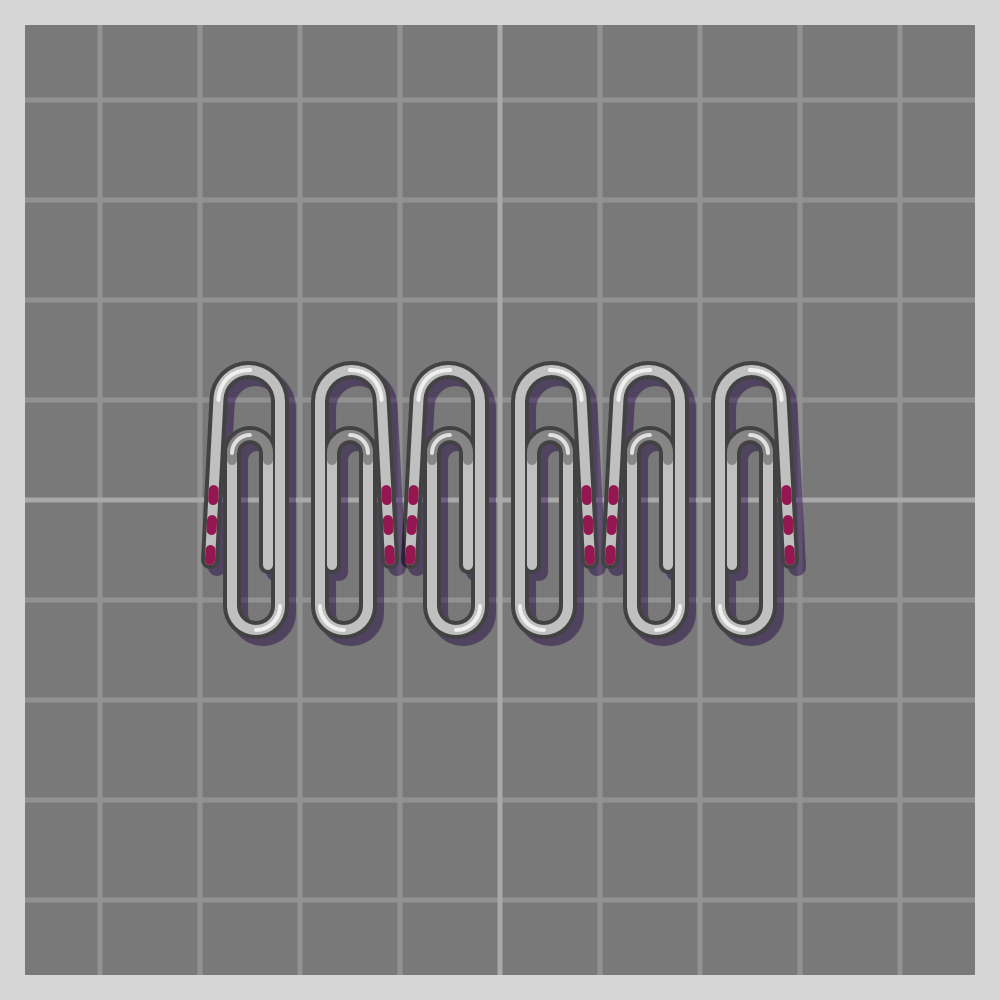
tg
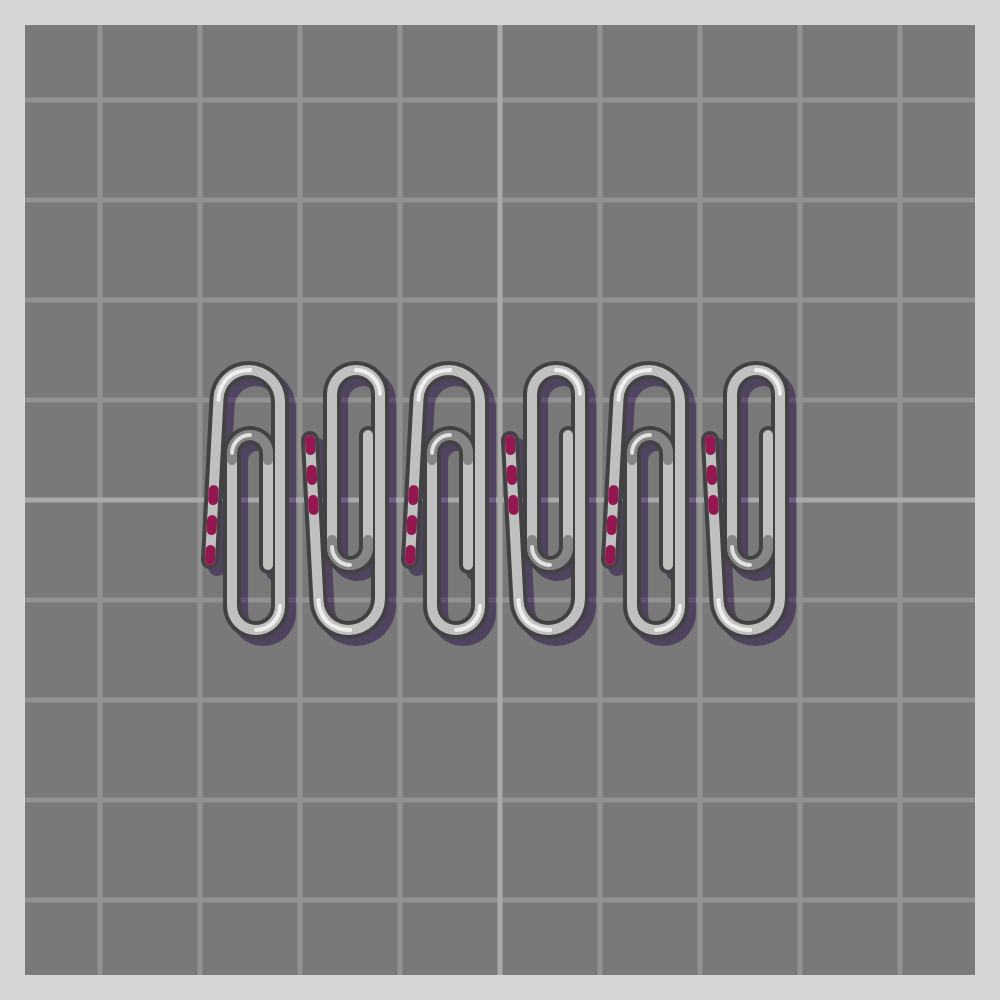
mt
t2
t2mg
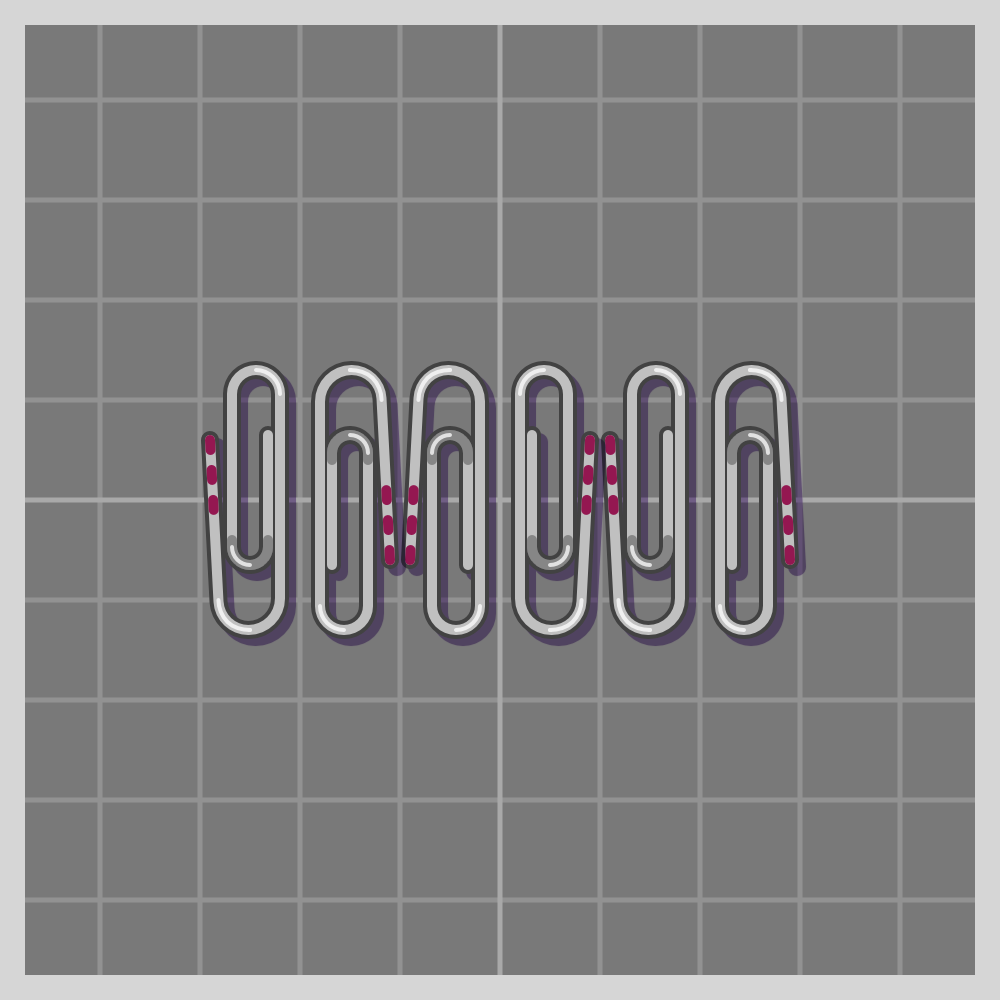
t2mm

Space Groups: Symmetries: Wallpaper (2-D)

Also known as “plane symmetry group” or “plane crystallographic group”. Wikipedia has a guide to recognizing wallpaper groups.

p1
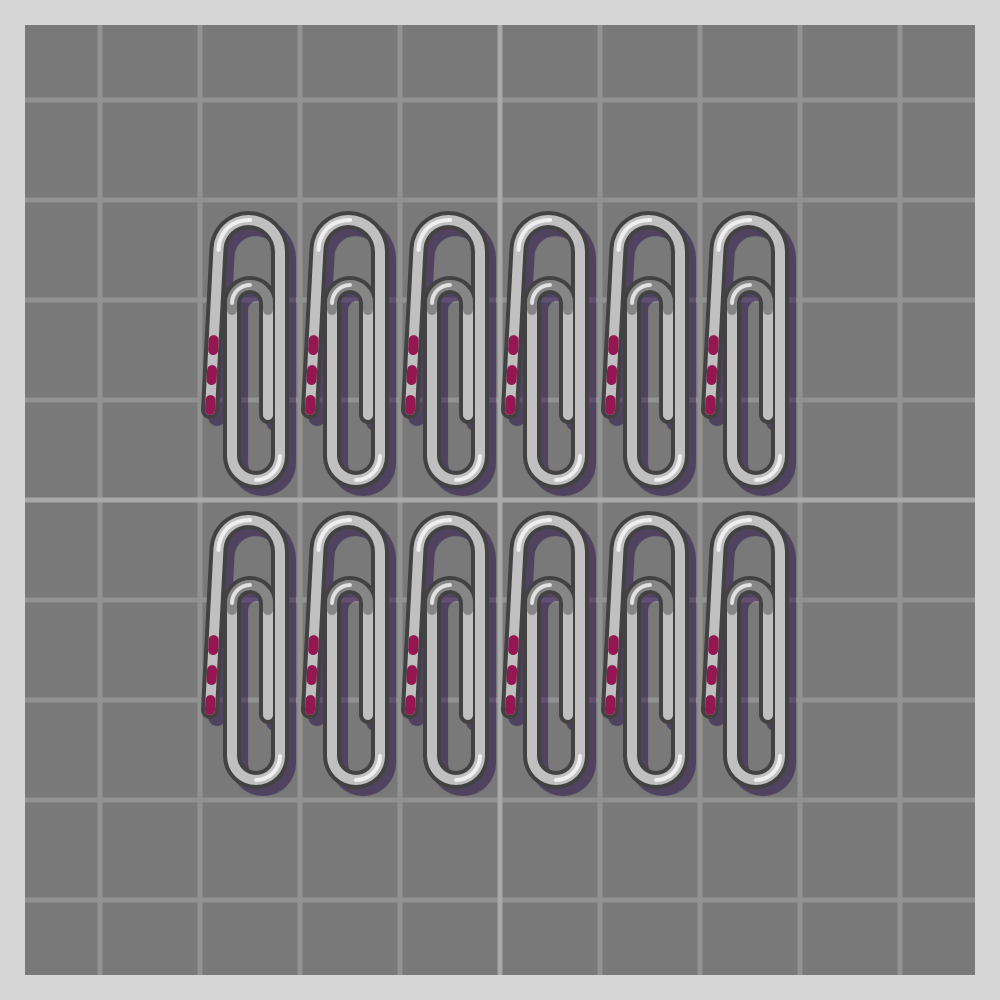
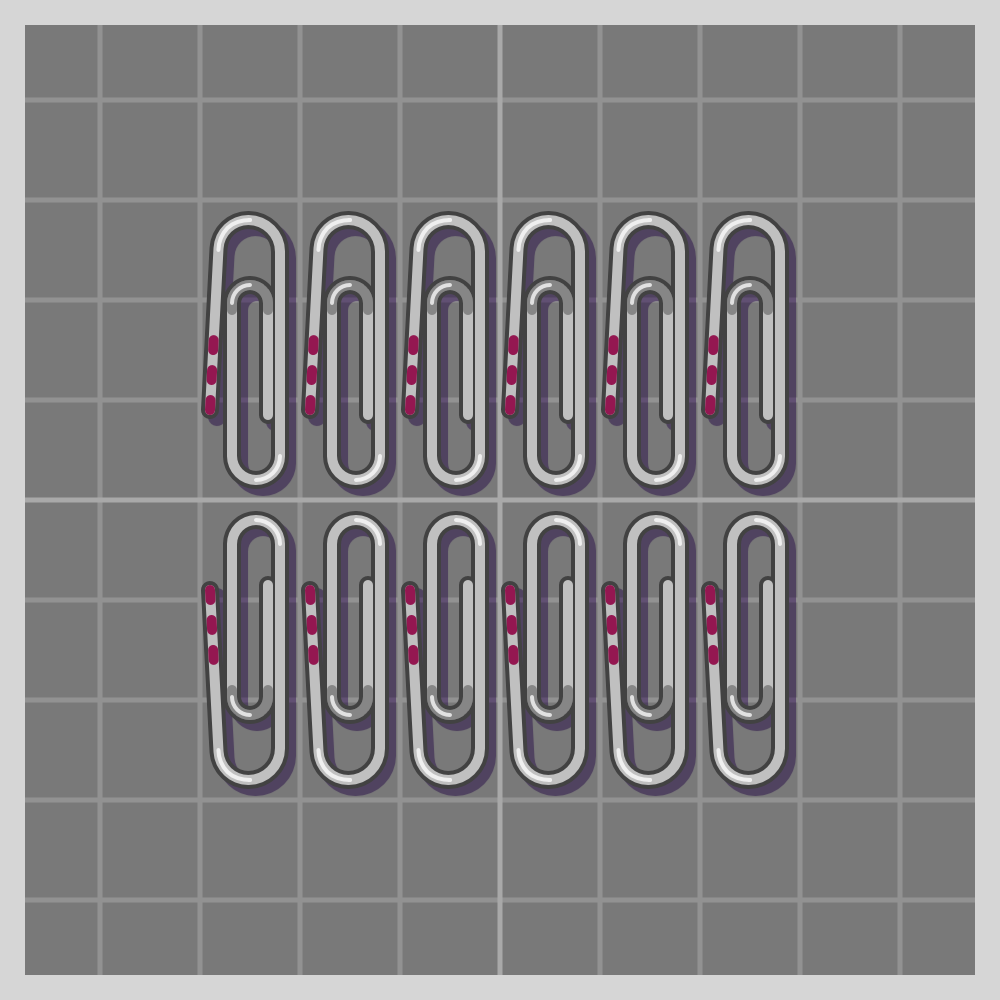
pm
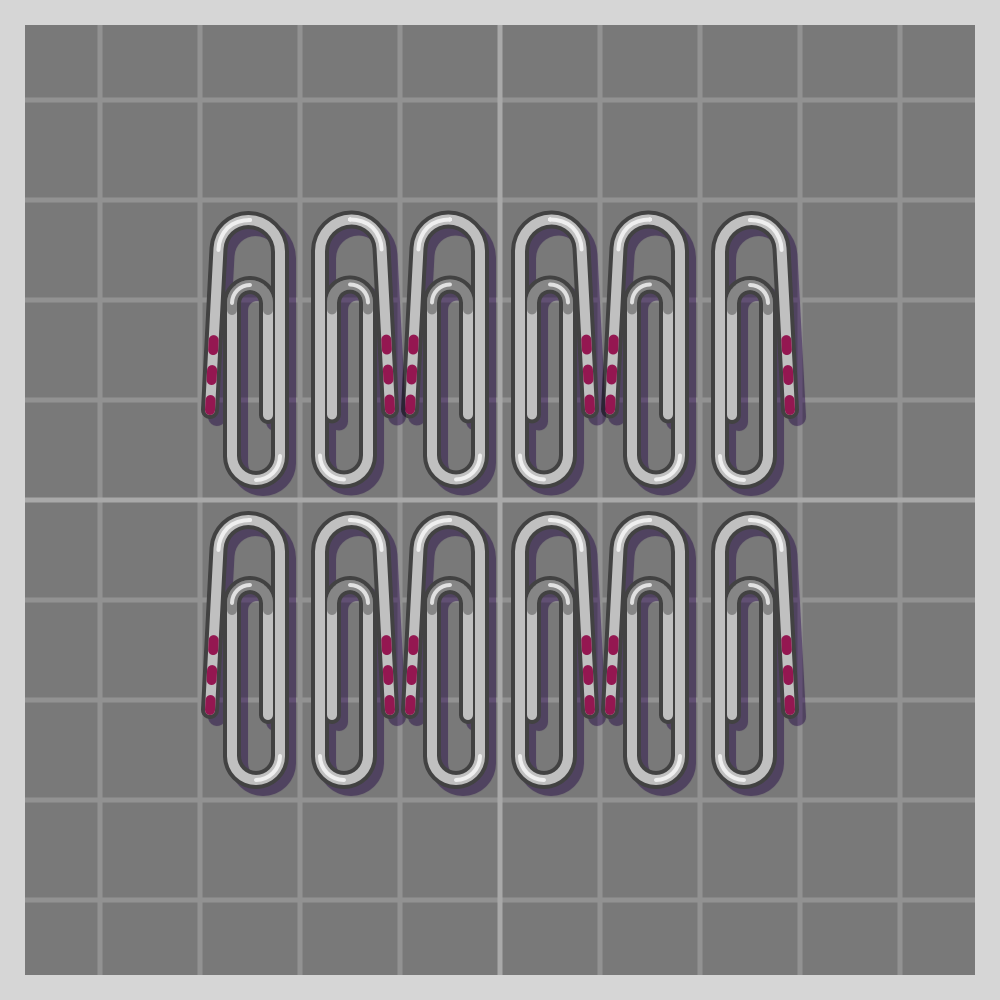
pg
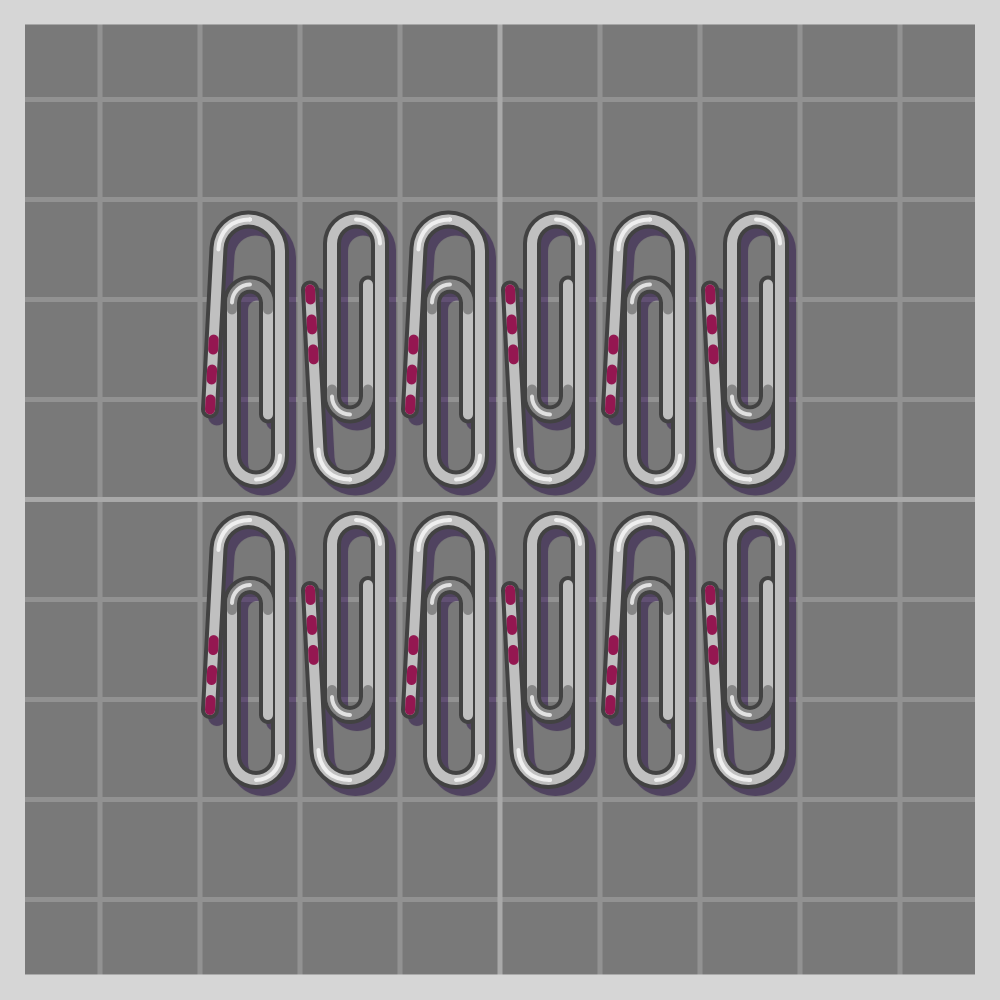
cm
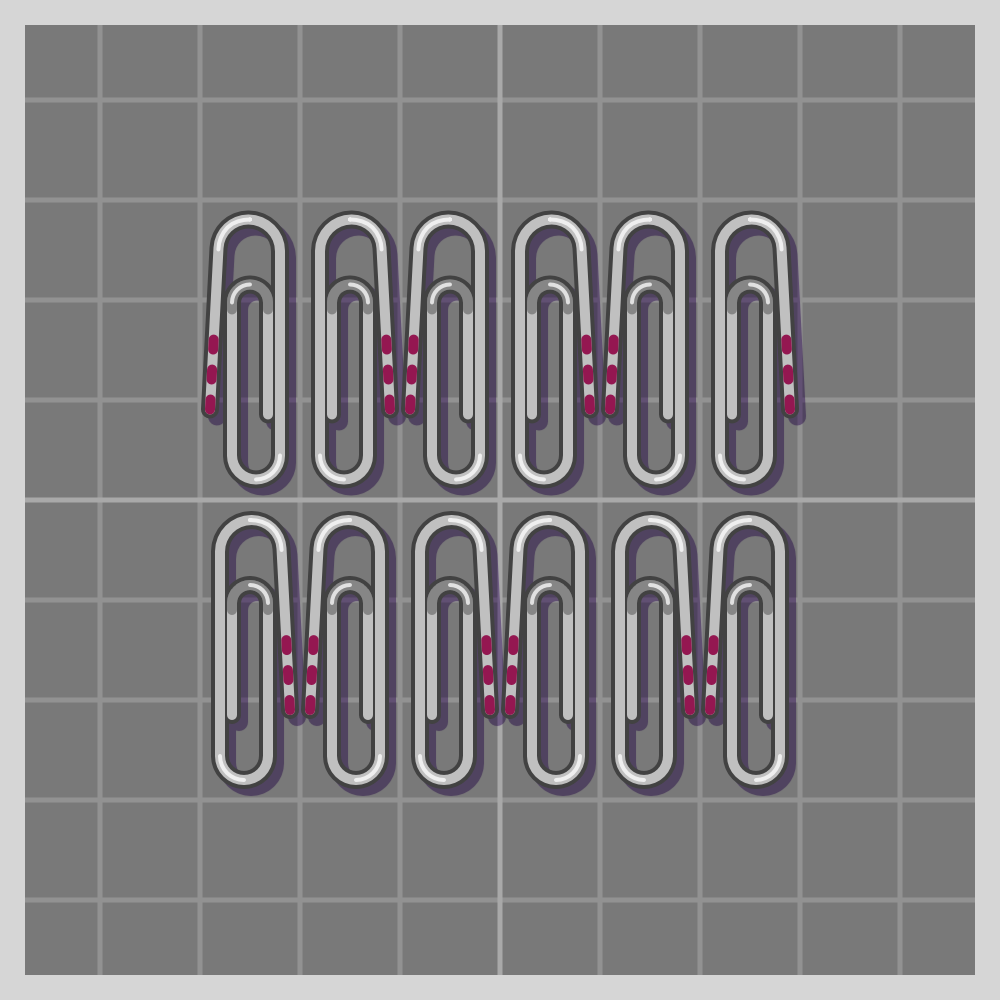
p2
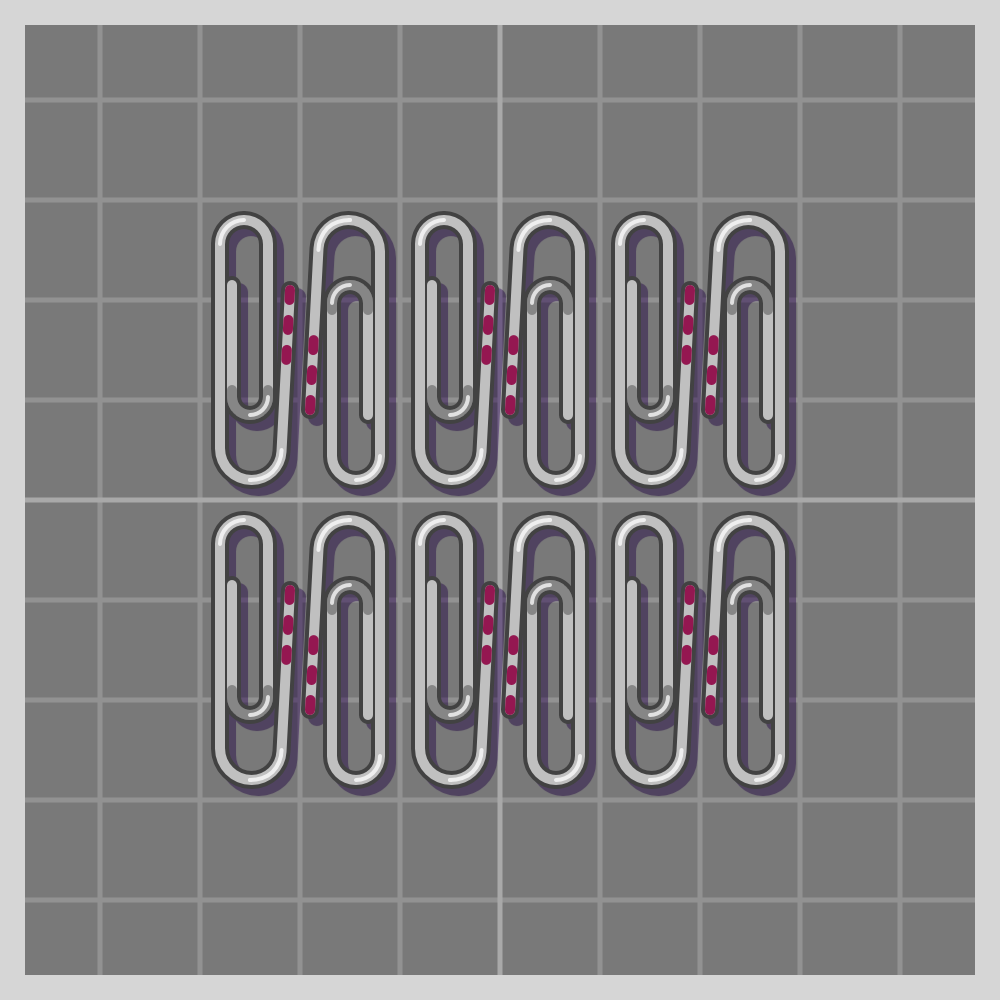
pmg (p2mg)
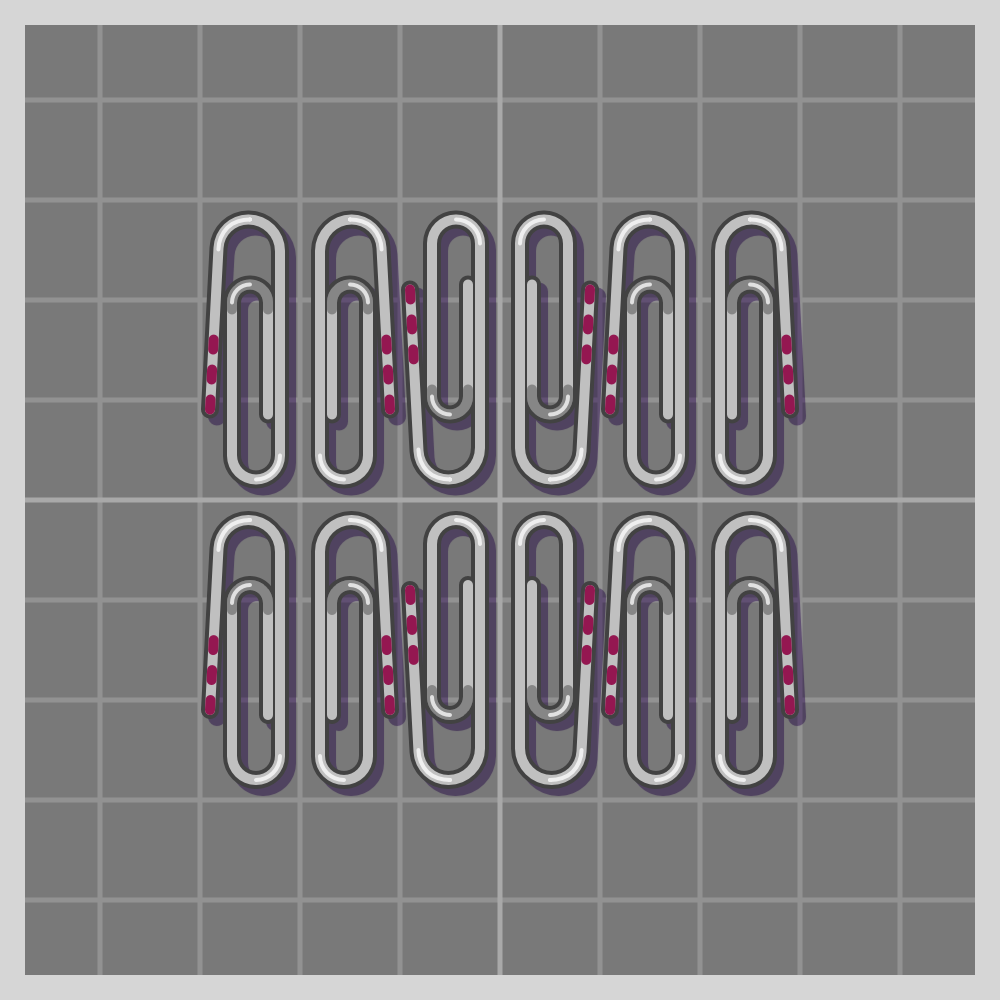
pgg (p2gg)
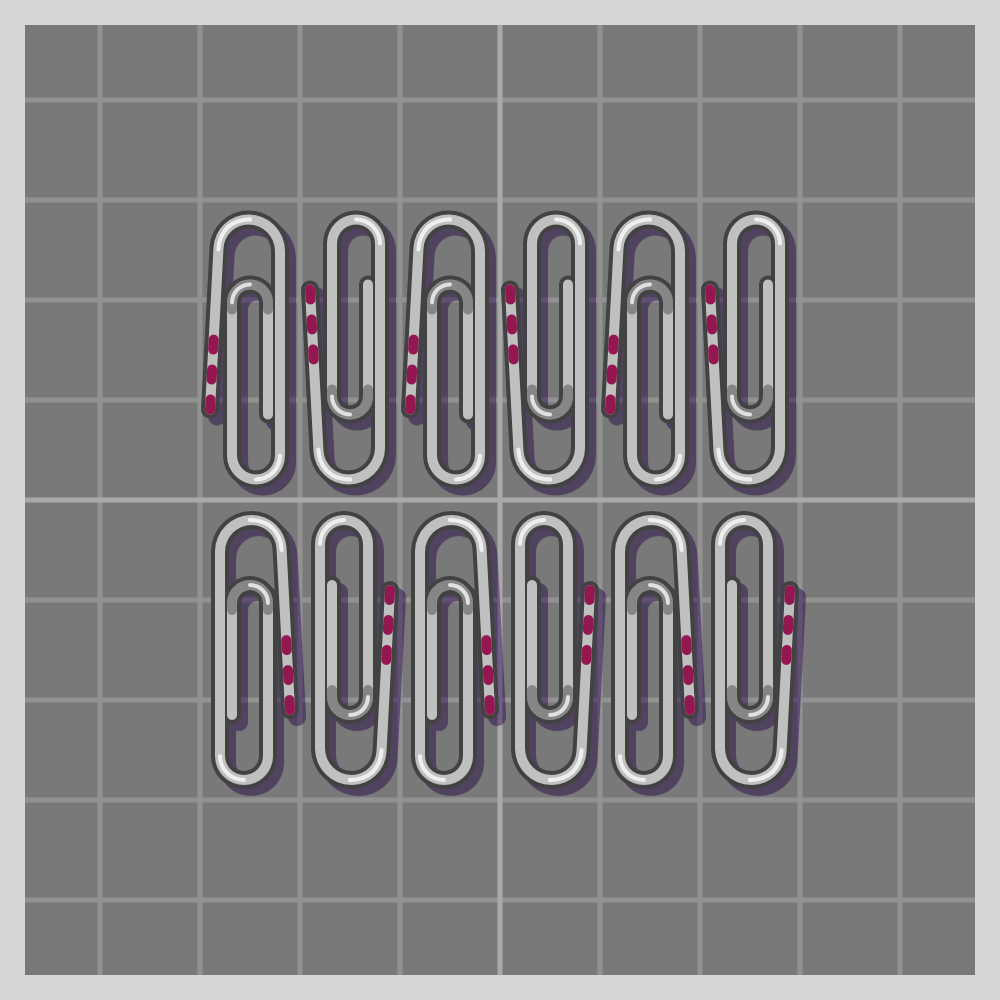
pmm (p2mm)
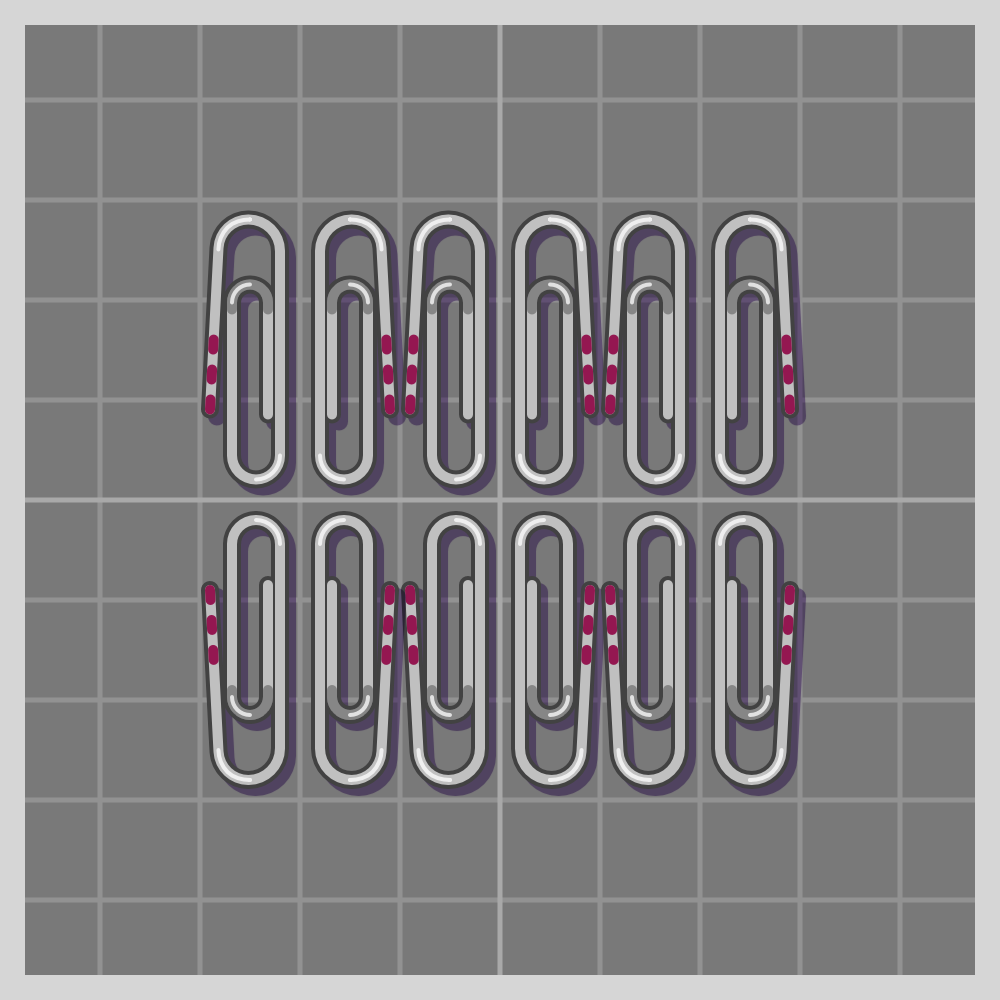
cmm (c2mm)
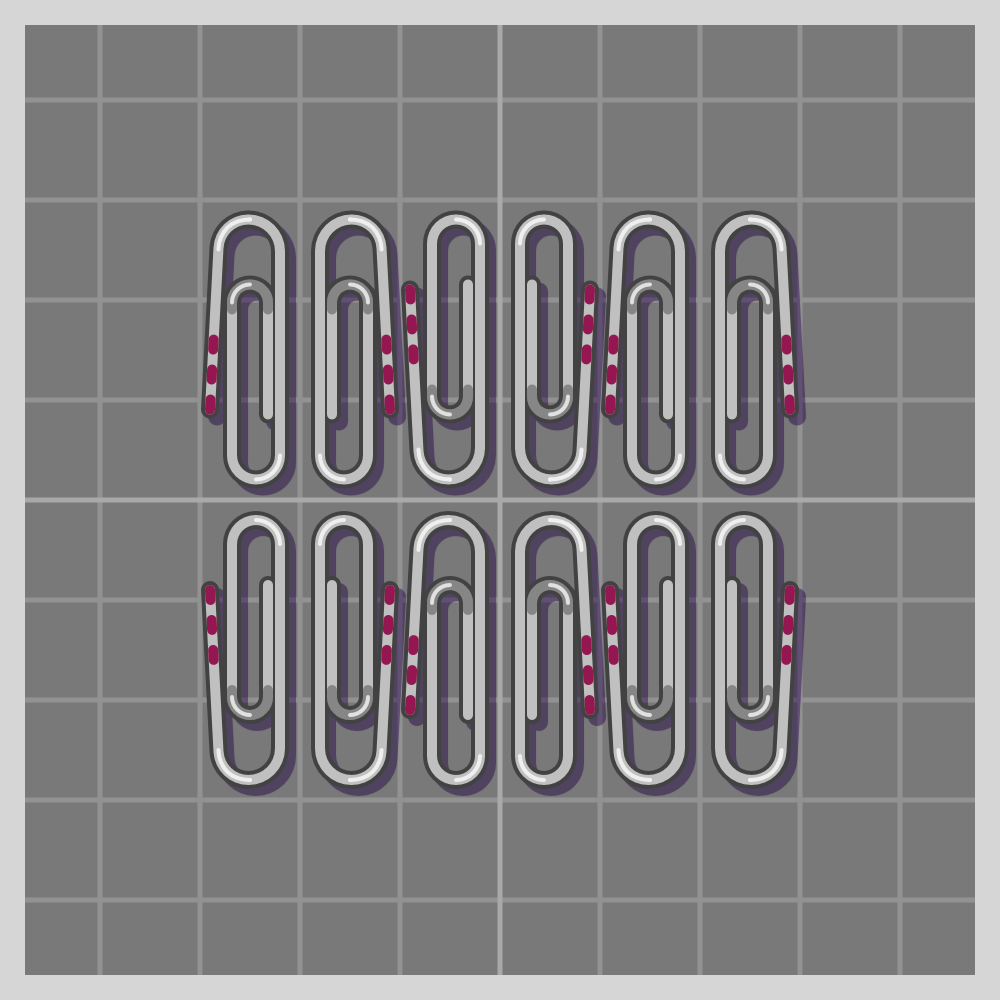
p3
p3m1
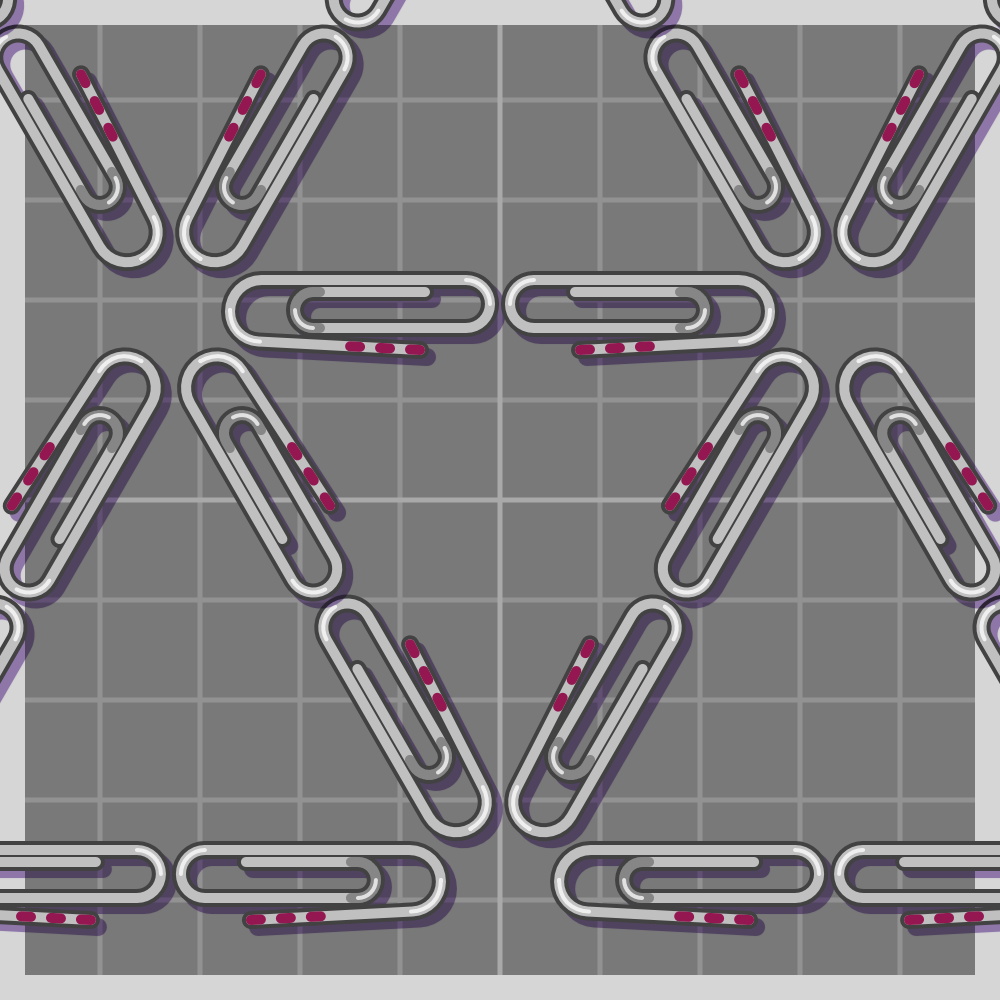
p31m
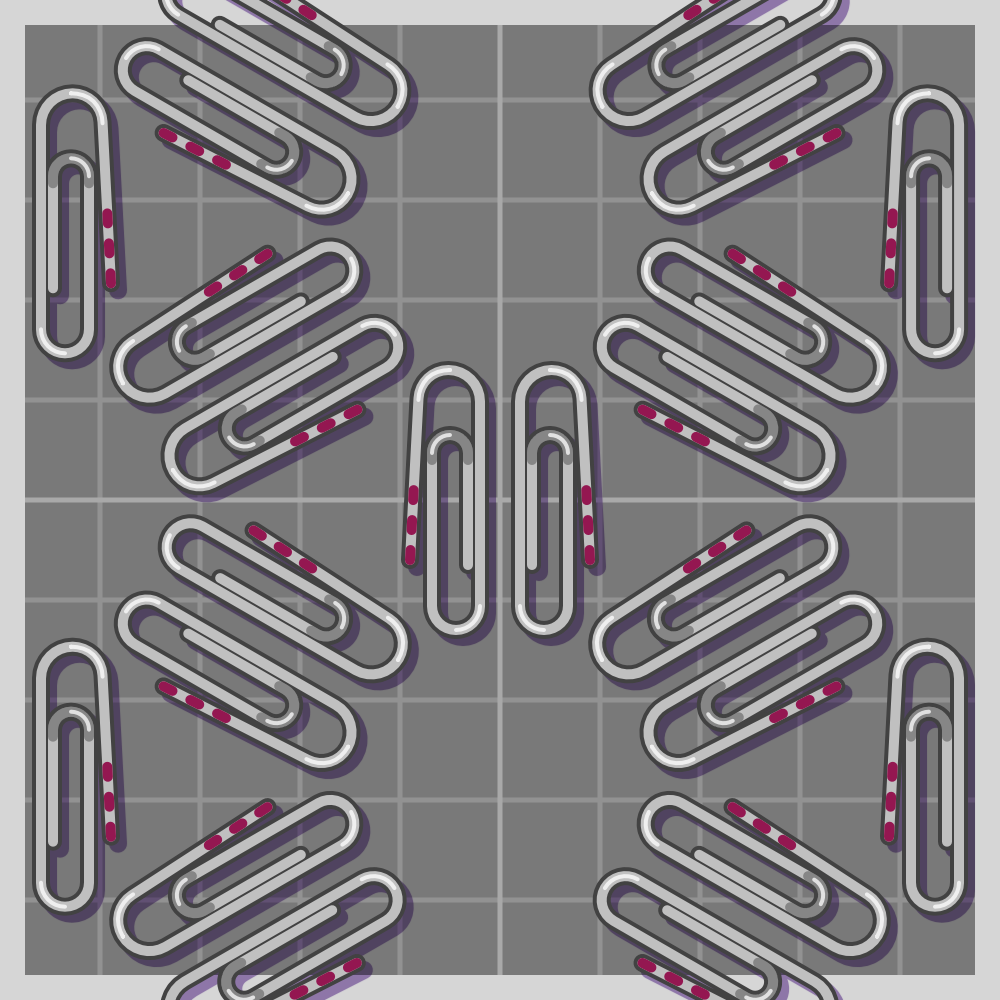
p4
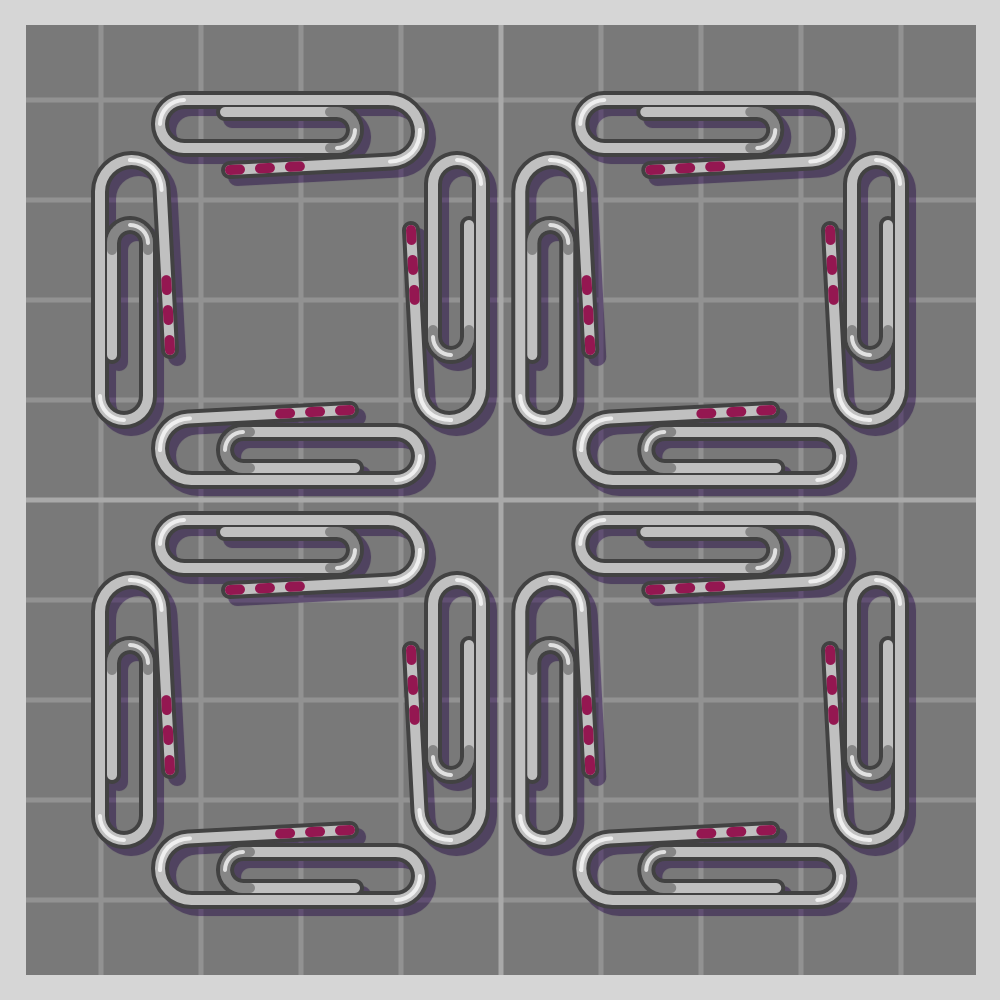
p4g (p4gm)
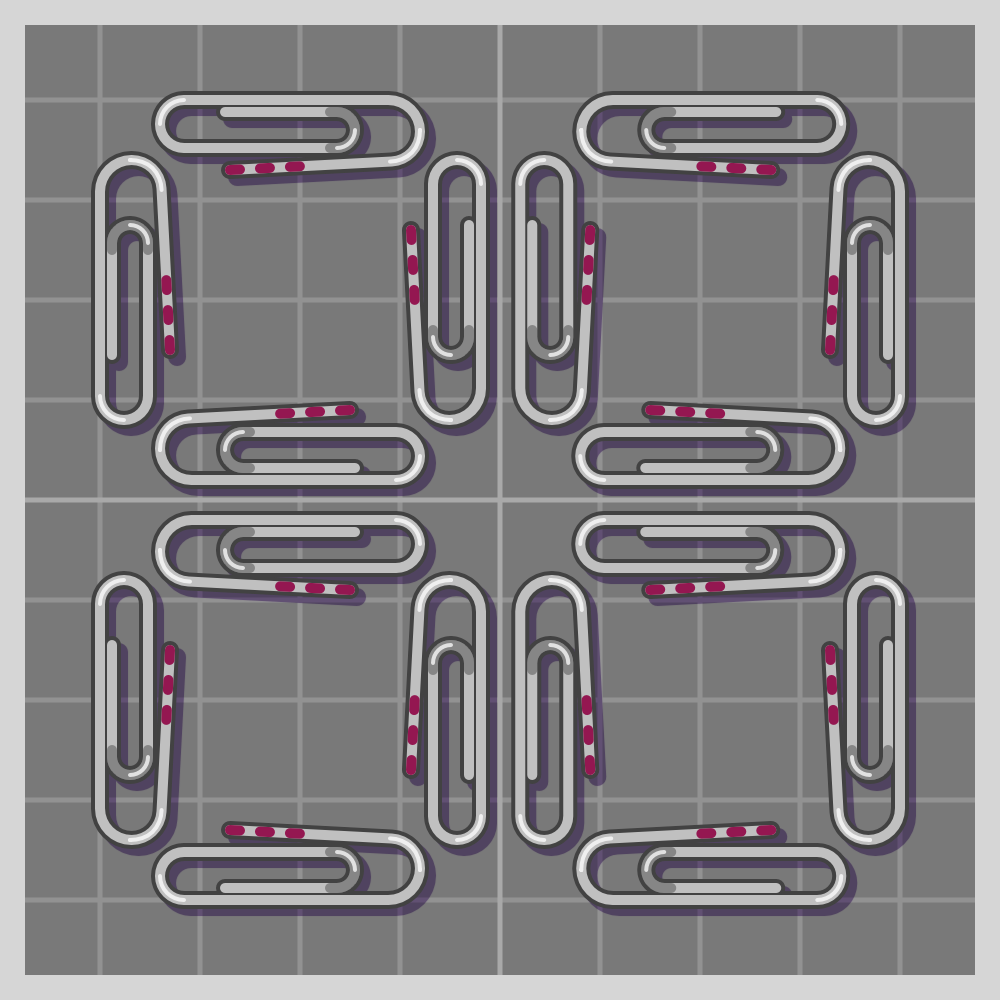
p4m (p4mm)
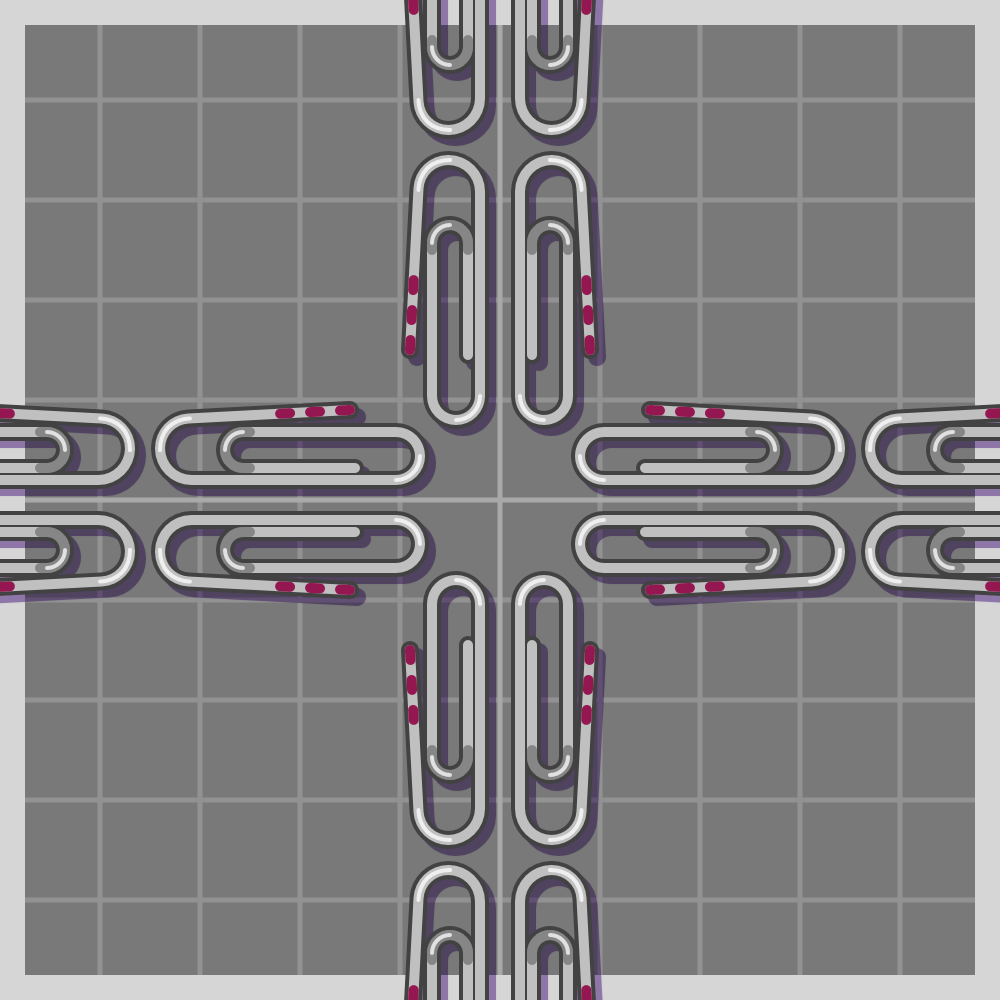
p6
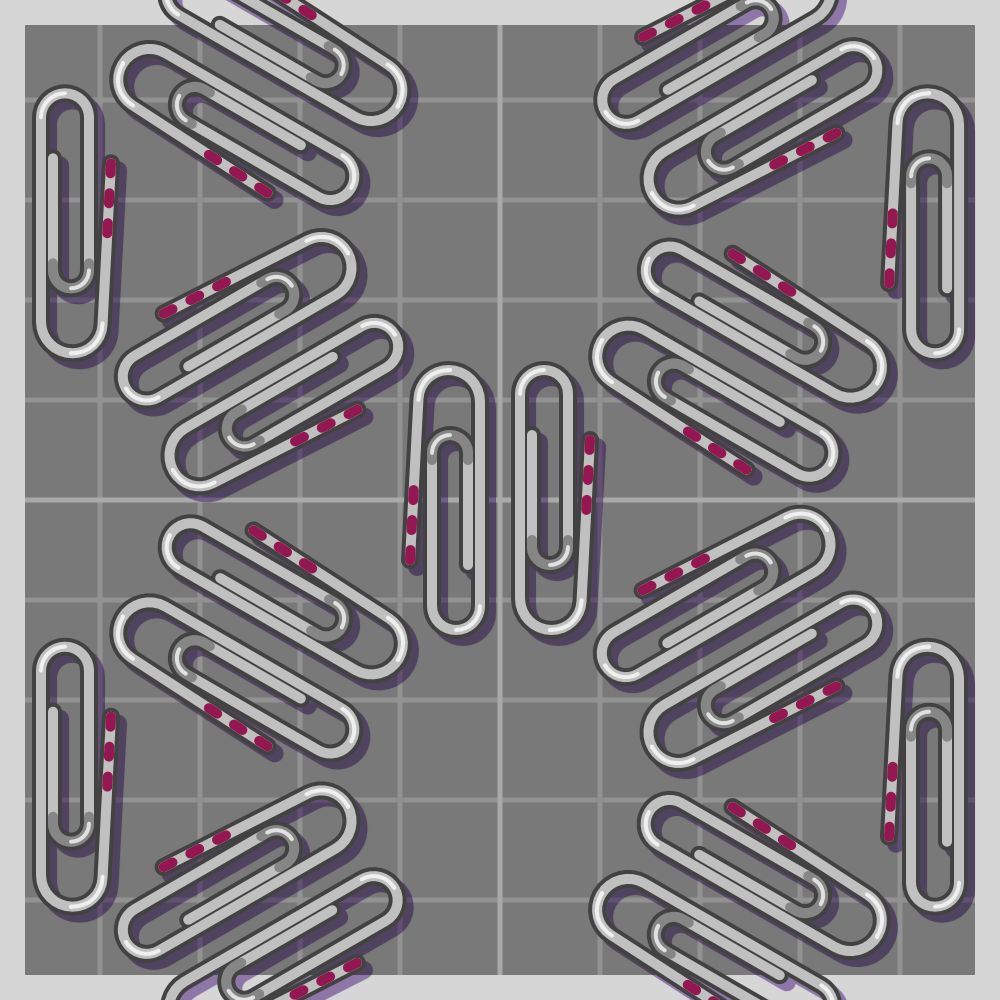
p6m (p6mm)

Further questions

Why are there “Glide Reflections” but no “Glide Rotations”?
- Can Rotation+Reflection be entirely done with Reflection by changing the location of the reflection plane?
- Apparently, the combination of rotation and reflection is called Improper rotation, and it is predicated on “a rotation about an axis and a reflection in a plane perpendicular to that axis.” This definition implies the need for three dimensions.
What about Scaling? Why isn’t this transformation part of the symmetry categories? Escher did use those in many of his art.
- Referred in Wikipedia as Scale Invariance